|
�n��FEM��̓G���W�j�A�����O�̂��߂̓���u����9��ڂł��B����́A��8�́u����f���x�ጸ�@�ɂ������́v�ɂ��Đ������܂��B����f���x�ጸ�@�ɂ������̗͂L�����A�܂��A���_�ɂ��Ă����������Ǝv���܂��B
�]���A�Ζʈ���͕����@�ɑ�\�����Ɍ����t�@��p���ĕ]������Ă������A�����@�ɂ͈ȉ��̂Q�̒Z��������B
- �z�肷��j��ʁi�܂��͉��z�j��ʁj��̕s�Ò�ȉ��͕��z�����߂邽�߁A�y��𑽂��̃X���C�X�ɕ����A�e�X���C�X�ɂ��ĐÒ艻���������肵�Ȃ���Ȃ�Ȃ��B
- ���ׂ�ʂ������Ȃ��ꍇ�A�ŏ����S�����������ׂ�ʂ��~���S�ʒu�A���a�����肵�ĒT������K�v������B
�{�͂ł́A�����@�����̂Q�̒Z�����ɍ������邽�߂̗L���Ȏ�@�ł���u����f���x�ጸ�L���v�f�@�iSSR-FEM�j�v�ɂ��Đ�������B
SSR-FEM�ɂ��Ζʈ����͂������s���Ă����BSSR-FEM�ł́A����f���x�萔 c ����� tanφ ��ጸ�W�� F �Ŋ������������̔S���� cF ����ь������̓������C�p φF �����̂悤�ɕ\�����B
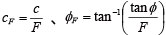 |
|
�i1�j |
SSR-FEM�ł́A��ʂɒe���S�Y�����f����p���ĉ��͂��v�Z����B�e���S�Y�����f���ł́A�������̔S���� cF ����ь������̓������C�pφF ��p���Ē�`����郂�[���E�N�[�������𗘗p���āA�y�̔j�� f �����̂悤�ɕ\���B
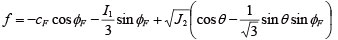 |
|
�i2�j |
�����ŁAI1�͉��͂̑�1�s�ϗʁAJ2�AJ3�͕����͂̑�2�A��3�s�ϗʁAθ ��Lode�p�ł���B
�܂��A�Y���|�e���V������Drucker-Prager������`����B
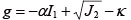 |
|
�i3�j |
�����ŁA
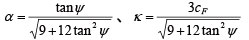 |
|
�i4�j |
ψ �͓y�̃_�C���C�^���V�[�p�ł���B�Ζʕ���������ƁA���ׂ�ʏ�ł͖c�������k���N����Ȃ���Ԃɋ߂Â��ƍl������̂ŁAψ = 0�Ɖ��肵���ق��������ɂ��߂��Ǝv����B����A�Ɍ����t�@��SSR-FEM�ɂ��S�̈��S�����r����ꍇ�ɂ́A�֘A���ꑥ�iψ = φF�j�����肵���ق����悢���Ƃ��킩���Ă���B
�e�Y���v�Z�ŕK�v�Ȓe���}�g���b�N�X�̓����O�W���ƃ|�A�\�����p���Ē�`����B�����̌W�����j��O�̕ό`�ɗ^����e���͑傫�����A�S�̈��S���ɋy�ڂ��e���͔��ɏ������B���������āA�y�̓����Ɋւ�炸�A�ꗥ�Ƀ����O�W����2×105kPa�A�|�A�\�����0.3�Ƃ��邱�Ƃ��ł���B
�]����SSR-FEM�ł́A�������̔S���� cF ����ь������̓������C�p φF ��p���āA����̍ő�J�Ԃ����ŁA�Ζʂ͓y�̎��d�Ȃǂ��O�͂Ƃ��Ēe�Y����͂������ł��邩�ۂ����`�F�b�N���A�v�Z�������ł���ő�̒ጸ�W�� F ���Ζʂ̑S�̈��S���ƒ�`�����B�]����SSR-FEM����荂���x�������ɑS�̈��S�����v�Z���邽�߂ɁA���͐V�����v�Z�A���S���Y�����Ă����B
���̊T�v���������Ǝ��̂悤�ł���B�܂��A�ŏ��̌W�� F �������Ȓl�ɐݒ肷��ƁA cF ����� φF ���\���傫���Ȃ�̂ŁA�Ζʂ͂�����Ƃ���Œe�����͏�ԂƂȂ�B���� F �� ΔF ���i�K�I�ɑ��������Ă����ƁA���� F �̒l���Ƃ�Ƃ��A�}1�Ɏ����悤�ɁA�Ζʓ��̂���ʒu�i�Ⴆ�Γ_A�j�Ŕj�����͂��߁A�������� cF ����� φF �Œ�`���郂�[���E�N�[�����̔j���i����2�j�����悤�ɂȂ�B
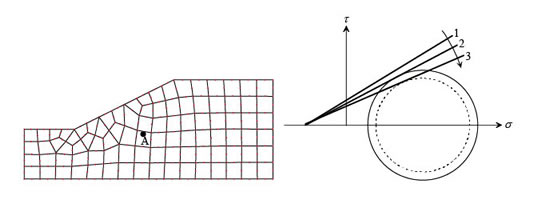 �� ���}1�@����f���x�ጸ�L���v�f�@�iSSR-FEM�j
F ������ɑ���������ƁA�_A�ł̎����̃��[���~�͔j���i����3�j�ƌ�������悤�ɂȂ�B���̂悤�ȉ��͏�Ԃ͑��݂����Ȃ��̂ŁA�}1�̔j���̉~�Ŏ����悤�Ƀ��[���~���j���ɐڂ���悤�ȉ��͏�ԂłȂ���Ȃ�Ȃ��B�X�e�b�v n �ɂ�����v�Z�������������_�ł́A�Ζʂ��͂̂荇����Ԃɂ��邽�߁A�c���̓x�N�g���̓[���ł���B
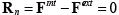 |
|
�i5�j |
�����ŁAFint�͓��̓x�N�g���AFext�O�̓x�N�g���ł���B���̓x�N�g���͎��̂悤�ɋ��߂���B
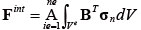 |
|
�i6�j |
�����ŁA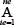 �͑S�v�f�� ne �̐������d�ˍ��킹�邱�Ƃ��Ӗ�����BB �͕ψʂ��Ђ��݂ɕϊ�����}�g���b�N�X�ł���B �X�e�b�v n �ɂ����āA�v�Z���������鎞�_�ł̉��� σn �͎��̂悤�ɗ^������B �͑S�v�f�� ne �̐������d�ˍ��킹�邱�Ƃ��Ӗ�����BB �͕ψʂ��Ђ��݂ɕϊ�����}�g���b�N�X�ł���B �X�e�b�v n �ɂ����āA�v�Z���������鎞�_�ł̉��� σn �͎��̂悤�ɗ^������B
�X�e�b�v n �ɂ����āA�v�Z���������鎞�_�ł̉��� σn �͎��̂悤�ɗ^������B
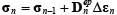 |
|
�i7�j |
�����ŁAσn-1 �̓X�e�b�v n-1 �ł̌v�Z���������鎞�_�ł̉��͂ł���B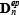 �̓X�e�b�v n �ł̒ጸ�W��Fn�ɑΉ����錩�����̔S���� cF ����ѓ������C�p φF ��p���Čv�Z�����e�Y���}�g���b�N�X�ł���BΔεn�̓X�e�b�v n �ł̂Ђ��ݑ����ł���B �̓X�e�b�v n �ł̒ጸ�W��Fn�ɑΉ����錩�����̔S���� cF ����ѓ������C�p φF ��p���Čv�Z�����e�Y���}�g���b�N�X�ł���BΔεn�̓X�e�b�v n �ł̂Ђ��ݑ����ł���B
�X�e�b�v n �ɂ����Čv�Z����������ƁA�X�e�b�v n +1�̌v�Z���n�܂�B�܂��O�X�e�b�v n �ł̂Ђ��ݑ���Δεn����ђጸ�W�� Fn+1 �ɑΉ����錩�����̔S����cF ����ѓ������C�p φF �ɂ��v�Z�����e�Y���}�g���b�N�X�ł���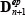 ��p���āA�X�e�b�v n +1�ɂ����āA�J��Ԃ���0�ł���Ƃ��̉��͂������Ōv�Z����B ��p���āA�X�e�b�v n +1�ɂ����āA�J��Ԃ���0�ł���Ƃ��̉��͂������Ōv�Z����B
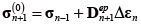 |
|
�i8�j |
�X�e�b�v n ����уX�e�b�v n +1�ł̒e�Y���}�g���b�N�X���Ⴄ���߁A ����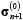 ��σn �͈قȂ�B�]���� ��σn �͈قȂ�B�]����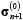 ��p���ē��̓x�N�g�����v�Z���� �ƁA�c���̓x�N�g���̓[���ł͂Ȃ��B ��p���ē��̓x�N�g�����v�Z���� �ƁA�c���̓x�N�g���̓[���ł͂Ȃ��B
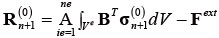 |
|
�i9�j |
���i9�j�Ōv�Z�����c���͔͂j�Ă��Ȃ��v�f�ɍĔz�����Ȃ���� �Ȃ�Ȃ��B�J�Ԃ��v�Z�ɂ��c���͂̍Ĕz���͎c���͂����e�덷��� �������Ȃ�܂ő����B���̎c���͂̍Ĕz���ɂ��j�����Ă���v�f�������Ȃ�B
�������� F �����X�ɑ��������Ă����ƁC�c���͂̍Ĕz���ɗv����J�Ԃ��v�Z�̉������Ă����B����i�K�Ŏc���͂̍Ĕz���ɗv����J�Ԃ��v�Z�̉�����l�i�Ⴆ��500��j���Ă��C�c���͂����e�덷�͈͓��Ɏ��܂�Ȃ���C�c���͂̍Ĕz���ɍ�������Ă���C�e�Y���v�Z�����U�����ƍl������B���̂Ƃ��Ζʂ̕ό`�͔��ɑ傫���Ȃ��Ă���C�Ζʕ���Ɏ������Ɣ��f�����B�Ζʂ̑S�̈��S���́C�J�Ԃ��v�Z���������Ȃ��Ƃ��̌W�� F �̒l�Ƃ��̒��O�� F �̒l�̊Ԃɂ���ƍl������B�v�Z�̃t���[�`���[�g��}2�Ɏ����B
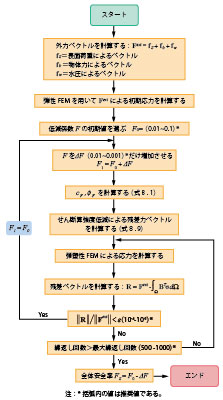 ��
���}2�@����f���x�ጸ�L���v�f�@�̃t���[�`���[�g
�L�����͂ŎΖʂ̈��萫��]������ꍇ�ɂ́A�����ΐZ������͂������͘A����͂ɂ�萅�����v�Z����B�Z������͂�A����͂ɂ�����SSR-FEM�Ɠ������b�V��������p����ƁA�Z������͂�A����͂œ���ꂽ�����������͂ɒ��ڎ������ނ��Ƃ��ł��邽�߁A��������萳�m�ɍl�����邱�Ƃ��ł���B
����ɁA���ׂ�ʂł͍ő傹��f�Ђ��݂̑������傫���Ȃ邽�߁A�ՊE���ׂ�ʂ͔j�O�̍ő傹��f�Ђ��ݑ����̕��z���琄��ł���B�]���āASSR-FEM�ł́A�����@�Ȃǂ̂悤�ɂ��炩���߂��ׂ�ʂ����肷��K�v���Ȃ��A�v�Z���ʂƂ��Ď����I�ɗՊE���ׂ�ʂ��T�������B
SSR-FEM�́A���x�̍������S�����Z��ł��邽�߁A�ׂ������b�V����p����K�v������B�܂������������C�Z�肵�����S���ɂ�����x�̉e����^���邱�Ƃ��킩���Ă���B�ߓ_�͎c���̃m�����Ɛߓ_�O�͂̃m�����Ƃ̔�́A�v�Z�X�e�b�v����J��Ԃ����ɉe������Ȃ����߁A���������Ƃ��čł��悭�g���Ă���B
SSR-FEM�͎Ζʈ����݂͂̂Ȃ炸�A�D���@��a�ǂ̈����́A�@���ʈ����́A�g���l���؉H�̈����͂ɂ��p�����A����������͂ɓK�p�ł�����@�ł���B
����܂ŁA�����@��SSR-FEM�ɂ�錋�ʂ��r���āA�Ζʈ���]���ɂ�����SSR-FEM�̗L�����͑����̕����Ɏ�����Ă���B�����ŁA���݂̂������Đ�������B����͐}3�Ɏ����悤�ɌX�����n�w�\�������Ζʂł���A�w①�Ƒw③�̊Ԃɂ���f���x���������w�A���͂��܂�Ă���B�w①�`③�̔S���͋y�ѓ������C�p�͂��ꂼ��29.4 kN/m2�A9.8 kN/m2�A294kN/m2�A�y��12°�A5°�A40°�ł���A�P�ʑ̐Ϗd�ʂ͋���18.82kN/m3�ł���B�����̌����҂͂��̗��p���ėl�X�ȕ����@����їՊE���ׂ�ʒT���@�������Ă����BSSR-FEM�ɂ��S�̈��S�����v�Z���A�j�O�̍ő傹��f�Ђ��ݑ����̕��z����ՊE���ׂ�ʈʒu�����肵���B�v�Z���ꂽ�S�̈��S����\1�Ɏ����B�}4�Ɏ����悤�ɁASSR-FEM�ɂ��ՊE���ׂ�ʂ́AGreco���T�������ՊE���ׂ�ʂƂ悭��v���Ă���B���ɎΖʓV�[�t�߂ɂ���ՊE���ׂ�ʂ̈ꕔ�͑w①�Ƒw②�̋��E�ʂɉ����Ă��邱�Ƃ��悭�\�����Ă���B�������Ȃ���A�����@��p���Ĉ��S�����v�Z���A�œK����@�ɂ��T������6�̗ՊE���ׂ�ʁi�����̂���4���}4�Ɏ�����Ă���j�̂����ASSR-FEM�ɂ��ՊE���ׂ�ʂƂقڈ�v�����̂́A2�i�����̂�������}4�Ɏ�����Ă���j�����Ȃ����Ƃ��킩��B���������āA��͂̑O�ɁA���ׂ�ʂ̌`������炩���߉��肷��K�v���Ȃ�SSR-FEM�̂悤�Ȉ����͖@�͑��̎�@�ɔ�ׂĂ��D�ʂɂ���ƍl������B
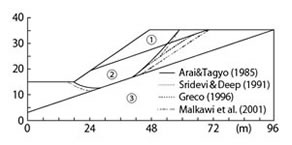
���}3�@�X�����n�w�\�������� |
|
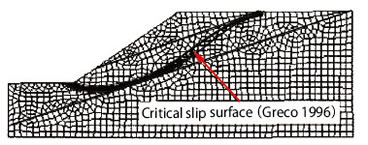
���}4�@�X�����n�w�\�������Ζʂ̗ՊE���ׂ�� |
���S���v�Z�@
|
�ՊE���ׂ�ʒT���@ |
�ՊE���ׂ�ʒT���@ |
�Q�l���� |
| �ȈՃ����u�@ |
�������z�@ |
0.405, 0.430* |
Arai��[1] |
| �ȈՃ����u�@ |
RST-2 |
0.401, 0.423* |
Sridevi��[2] |
| Spencer |
Pattern search |
0.38 |
Greco [3] |
| Spencer |
Monte Carlo |
0.38 |
| Spencer |
Monte Carlo |
0.401 |
Malkawi��[4] |
| Spencer |
Random search |
0.401 |
Rocscience Inc. [5] |
| �ȈՃ����u�@ |
Random search |
0.410, 0.434* |
| Spencer |
Random search |
0.44 |
Kim��[6] |
| Lower-bound |
- |
0.40 |
| Upper-bound |
- |
0.45 |
| SSRFEM (ψ = φ) |
- |
0.417 |
����[7] |
| SSRFEM (ψ = 0) |
- |
0.423 |
�i���j���F�ȈՃ����u�@�̈��S���ɏC���W�����悶�����̂ł���B
���\1�@�X�����n�w�\�������Ζʂ̑S�̈��S��
[1] Arai, K., and Tagyo, K.: Determination of noncircular slip surface giving the minimum factor of safety in slope stability analysis, �y���H�w��_���W, 25(1): 43-51, 1985.
[2] Sridevi, B., and Deep, K.: Application of global-optimization technique to slope-stability analysis, Proc. 6th Inter. Symp. on Landslides, pp.573-578, 1992.
[3] Greco, V. R.: Efficient Monte Carlo technique for locating critical slip surface, J. Geotech. Eng. Div., ASCE, 122(7): 517-525, 1996.
[4] Malkawi, A. I. H., Hassan, W. F., and Sarma, S. K.: Global search method for locating general slip surface using Monte Carlo techniques, J. Geotech. Geoenviron. Eng., 127(8):688-698, 2001.
[5] Rocksciemce Inc.: Verification manual for Slide, 2D limit equilibrium slope stability for soil and rock slopes, Version 4.0, Rockscience Inc., Canada, 2002.
[6] Kim, J., Salgado, R., and Lee, J.: Stability analysis of complex soil slopes using limit analysis, J. Geotech. Geoenviron. Eng., 128(7): 546-557, 2002.
[7] ��䖾�F�E���F�n���ׂ��͂ɂ�����L���v�f�@�̗��p ��4�� FEM�ɂ��n���ׂ��͂̊�b���_�A���{�n���ׂ�w��A40(3): 76-80�A2003.
���ɁA���А��i�ł���GeoFEAS2D��Post�\���ɂ��ď����Љ�����܂��B�}5��GeoFEAS2D�ɂ�邹��f���x�ጸ�@�̉�͌��ʉ�ʂł��B�R���^�}�̍ő�Ђ��ݑ����Ŋm�F���邱�Ƃ��ł��܂��B����́A��ʓI�Ȑ��y�`��ɂ��ĎΖʈ����͂��s������ł��B���ׂ��Ԃ��m�F�ł���Ɠ����ɁA��ʍ���̐Ԉ݂͂̒ʂ�A���S�������߂��܂��B
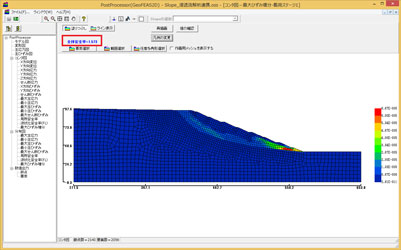 ��
���}5�@GeoFEAS2D�ɂ���͌��ʉ��
����́A�u����f���x�ጸ�@�ɂ������́v�ɂ��ĉ�����܂����B��藝����[�߂����ꍇ�́A���ЂŊJ�Â��Ă���L���Z�~�i�[�Ȃǂ������p�肢�����Ǝv���܂��B����́u�t�ɔ������d�ɂ��ό`��́v�ɂ��ďЉ�v���܂��B�͐�\�����̐v�ł͕K�{�̌����ƍl�����܂��B�����҉������B
�t�H�[�����G�C�g�p�u���b�V���O�̏��ЃV���[�Y
�w�V�� �n��FEM ��͓���x�̂��ē�
�n��FEM��͂Ɋւ���L�x�Ȍo���ƌ������тɗ��t����ꂽ�n�Չ�͓��发�B�n��FEM��͂̊�b���_�A���f�����O�Z�p�����A���l�ȉ�͎���ɂ��āAFEM��͂ɂ��������̃v���Z�X�ƌ��ʂ��킩��₷����������n�ՋZ�p�ҕK�g�̈���ł��B
���ďC�F�L�� �{�O�i�S���{�n���ׂ�w��,�Q�n��w�����j
�����ҁF�� ��i�Q�n��w�����j
��2013�N9��19�����s
��4�F�^245�y�[�W
��\3,800�i�ŕʁj
���t�H�[�����G�C�g �p�u���b�V���O��
�����Ђ̂��w���́A�t�H�[�����G�C�g�����T�C�g�܂���Amazon.co.jp�ŁI
|
 |
| �@���w�V�ŁE�n�� FEM��͓���x�ڎ��\�� |
| ��1�� |
�n�ՍH�w�ɂ�����FEM ���
�n��FEM��͂̕K�v���E�̌n�A��͎�ށA���l��͂̌덷 |
| ��2�� |
�n��FEM ��͂̊�b���_
�͊w�̊�b�A���ʂЂ��ݖ��Ǝ��Ώ̖��A�L���v�f�@�̊�b |
| ��3�� |
�n��FEM ��͂̂��߂̃��f�����O�Z�p
��͖ړI�A��@�A�����A�g���l���@���͂ɂ����鉞�͉���� |
| ��4�� |
�n�Սޗ��̍\����
���͕s�ϗʁA���`�e���\�����A����`�e���\���� �A�e���S�Y�����f���A�i�Y���\���� |
| ��5�� |
�ޗ��p�����[�^�̌��ߕ�
�������`�e���\�����A�e���S�Y�����f���A�j��ڋߓx�@�̃p�����[�^�̓�����@ |
| ��6�� |
�n�Ղƍ\�����̑��ݍ�p
�\�����̃��f�����A�C���^�[�t�F�C�X�̃��f���� |
| ��7�� |
����`���
�����@�ANewton-Raphson�@�A�J�Ԃ��v�Z�ɂ������������ |
| ��8�� |
����f���x�ጸ�@�ɂ�������
����f���x�ጸ�L���v�f�@�̏Љ�Ɖ��p�� |
| ��9�� |
�t�ɔ������d�ɂ��ό`���
��͎�@�A�p�����[�^�A��͎���A�_�\�����̐v�Ƃ̘A���@�\ |
| ��10�� |
��͎���
���y�̎Ζʈ���A �i�ǍY��b�̐��y�ډז��A�g���l���g���H���A���i�H�@�ɂ��n�Ղւ̉e����� |
| ��11�� |
GeoFEAS �̑�����@
�g���l���@��ɔ����ߐڍY��b�ւ̉e����́A����f���x�ጸ�@�ɂ��Ζʂ̈����� |
| ��12�� |
�n���M��͂ɂ���
�n���M�ɂ��āA�n���M��͂Ƃ� |
|