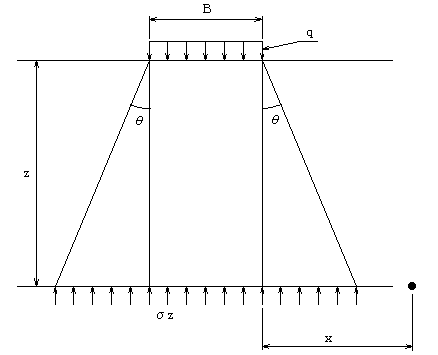
Q&A　（製品評価や導入の際に役立つQ&Aです） 　１．荷重 Ｑ１−１． 荷重データ入力項目の無限長帯荷重の分散角とは何か？ Ａ１−１． 地中応力の計算においては、ブーシネスク法での計算に際して地中応力の分散は、紡錘体状の分布を呈すものとしてプログラムにより自動計算します。一方、地中応力を慣用計算法（ボストン・コード法）での計算に際しては、地中における応力分布は一定角度におり直線分布するものとした計算になります。分散角とは、この慣用計算法（ボストン・コード法）における地中応力の鉛直面からの広がりを表す角度をいい、入力した任意の角度における地中応力を計算できます。 　　 　 Ｑ１−２． 荷重データ入力項目の無限長帯荷重の奥行きとは何か？ Ａ１−２． 本プログラムでは、圧縮変形（圧密沈下）の計算とせん断変形（即時沈下・側方変位）の計算とが行えます。　圧縮変形（圧密沈下）につきましては二次元計算（圧縮は鉛直方向のみ）であり、載荷重において奥行きはありません。一方、せん断変形（即時沈下・側方変位）の計算に際しては、せん断を発生させるため、載荷重は有限幅・有限奥行きである必要があります。　奥行きとは、このせん断変形（即時沈下・側方変位）を計算する際の載荷重の奥行き方向の長さのことを指します。 　 Ｑ１−３． 任意荷重は入力できるか？ Ａ１−３． 任意荷重の入力も可能です。 本プログラムにおける載荷重の入力形式の区分につきましてご説明いたします。 以下の(B)に示す[盛土データ]による入力につきましては、地中応力算出法としてオスターバーグ図法を選択した場合に対応する、地表面が水平な場合における台形形状での入力としてご用意しているものであり、定型形状の載荷となりますため、載荷面の凹凸に応じて形状が変化します。一方、以下の(A)に示す[荷重データ]による入力は、台形形状以外の任意形状の入力に相当します。 　(A) [入力]-[荷重データ] → 任意形状（：地表面に起伏に応じた入力） 　(B) [入力]-[盛土データ] → 台形（：地表面が水平であることが前提） つまり、台形以外の任意形状の入力を行う場合には、『上載荷重』であるか『盛土』であるかによらず、一律に上記(A)の荷重として入力して下さいますようお願い致します。 Page Top 　２．地盤 Ｑ２−１． 地表面の形状に凹凸があるときはどのように入力するのか？ Ａ２−１． [入力]-[地表面と地層幅]にて、中間点を入力することにより、地表面の凹凸を入力して下さい。 　 Ｑ２−２． 水位の考慮は可能か？ Ａ２−２． 「水位線」入力画面で水位線データを入力し、「土質データ」にて湿潤重量と飽和重量との2種類を入力します。飽和域と不飽和域との圧縮特性を変えたい場合には、適宜、□地下水位以下の土質データを変更するチェックボックスをチェックして、「土質データ（水位以下）」に異なる圧縮特性を入力することもできます。 Page Top 　３．その他 Ｑ３−１． 旧バージョンのデータファイル*.amiを開くにはどうしたらよいか？ Ａ３−１． 弊社では、データの共通化を図る目的から、ファイル形式をXML形式に統一しております。その経緯から、最新版では、XML形式（拡張子f8t）のみに対応しております。 旧々々版 ：保存形式はバイナリ形式ファイル（拡張子AATI） 旧々版 ：保存形式はバイナリ形式ファイル（拡張子ATIor拡張子AATI） 旧版Ver.3.00.05以前 ：保存形式はバイナリ形式ファイル（拡張子AMIor拡張子ATIor拡張子AATI） 旧版Ver.3.01.00以降 ：バイナリ形式・XML形式との双方の保存に対応。 Ver.4.00.00以降 ：読込み・保存ともXML形式ファイル（拡張子f8t）のみ。 お手数ですが、下記の手順にてVer.2形式データファイル（*.AMI）を最新版形式にコンバートしてご使用下さい。 旧々バージョンデータファイルの最新バージョン形式への変換手順： 「圧密沈下の計算Ver.3.01.××」にて（*.AMI）を読み込み、（*.f8t）形式で保存 「圧密沈下の計算Ver.5」にて（*.f8t）を読み込む。 Ver.3.01.00以降のプログラムで読み込み（最終版はVer.3.01.02）、保存しなおすことで対応くださいますようお願いいたします。 Page Top 　４．対策工 Ｑ４−１． 盛土の除去設計はできるのか？ Ａ４−１． はい、本製品では設計条件として予圧密工法を選択することにより、荷重除去の設計が可能です。 但し、通常のプレロードによる荷重除去による設計は可能ですが、サーチャージ工法での計算は直接は出来ませんのでご注意ください。 つまり、プレロード荷重を全て除去した場合での計算は可能ですが、余盛分だけを除去する計算に対応しておりません。 サーチャージ工法での設計手段としては、載荷荷重に負の荷重を入力するのではなく、施工段階を分けて、設計していただくなどの設計者の判断が必要となります。 設計方法としては、載荷盛り土の終了時点における圧密計算結果を利用していただき、次にその時点での層厚と各諸元データを入力した設計データを再入力し、最後にそのデータに対して構造物と活荷重を載荷設計する方法などが考えられます。 しかし、粘性土の特性は、載荷荷重により圧密降伏応力を越える状況となった場合は、正規圧密状態へ移行し圧密が開始され、その荷重により圧密が収束すれば同じ荷重では沈下は生じません。その途中で荷重を除去した場合、除去荷重が圧密降伏応力を越えており、かつ圧密が収束していれば、それ以上の沈下は生じないことになります。 一方、沈下が収束していない際には、除荷後再載荷によって沈下を生じる場合があり、この様な場合の圧密降伏応力は、設計者が圧密の応力度などから別途算出する必用が有ります。 従って、圧密は増加荷重により計算されるものですが、除荷後に載荷される総荷重がこれを越えるもので有れば、盛り土荷重は設計に影響が生じることになります。 　 Ｑ４−２． 地盤改良を考慮できるか？ Ａ４−２． 本プログラムでは、地盤改良率（例えばソイルセメントとする場合の配合等）の入力により、改良後の物性を自動計算し、それに基づいて改良後の沈下を計算する仕組みにはなっておりません。 改良後の地盤の物性につきましては、設計基準類にも規定はなく、ユーザー様ご自身で設定していただく他はございません。 ソイルセメントのような強固な改良を行うのであれば、当該箇所は沈下しないとして、未改良部のみの沈下のみを照査するということで良いと思われますが、改良の程度により改良部の沈下を見込みたい場合には、適宜物性値を仮定して下さい。 　 Ｑ４−３． 緩速載荷でクリティカルでない層はどのように計算しているのか？中詰め土の地震時慣性力の扱いは？ Ａ４−３． 全ての層に対して同じ緩速載荷の計算理論が適用されます。 但し、施工期間中に圧密が終了してしまうような過大な圧密係数である層に対しては、この緩速載荷の計算理論の適用範囲外になりますため、施工期間中の経時変化が線形的な変化として出力されますが、これは理論解がこのようになるというのではなく、理論の適用範囲外であるためと理解すべきでしょう。 　 Ｑ４−４． 自然圧密の場合と圧密促進工法の場合とで、層の出力が異なるどういう意味か？ Ａ４−４． 層厚換算法により、連続する粘性土層を一つの圧密層に換算するのは、鉛直排水となる自然圧密時のみであり、水平排水となる圧密促進工法につきましては、層厚換算は行われませんので、ご注意下さい。 (a) 自然圧密 　　　→　地盤全体が鉛直排水するとしてTerzaghiの圧密方程式を解法 　　　→　層厚換算法により、深さ方向に連続する粘性土層を一つの圧密層に換算して、解法します。 (b) 圧密促進 　　　→　地盤全体が水平排水するとしてBarronの式の解法（ウェルレジスタンス非考慮） 　　　→　地盤全体が水平排水するとして吉国の式の解法（ウェルレジスタンス考慮） 　　　→　水平排水であるため、層厚換算は行わず、各粘性土層ごとに解法します。 計算につきましては、層ごとにウェルレジスタンスを考慮しない場合には、Barronの式を解法し、ウェルレジスタンスを考慮する場合には吉国の式を解法しています。全層における圧密過程は重ね合せ法により、各層ごとの結果の単純和としています。 　 Ｑ４−５． ディープウェルや、ウェルポイント工法での揚水を行った場合の地下水低下における沈下量を算定することが出来るか？ Ａ４−５． 当該機能はお問い合せにありますようなディープウェルに起因して発生する圧密沈下現象の解法に対して適用できるよう開発した機能です。 圧密沈下の発生メカニズムにつきまして、以下にご説明します。 　　(a) 盛土重量により下層の間隙水が押し出される圧密沈下 　　(b) 地下水低下により間隙水が吸い出される圧密沈下 上記(a)の現象では、飽和土に圧力（力）が加わった際に、間隙水がしぼり出され、土が圧縮されることにより、圧密沈下が発生します。一方、上記(b)の現象では、地下水位が低下すると、土が受けていた浮力が無くなることにより土の重さが増し、土に圧力が加わった際と同様の現象が生じて土が圧縮され、この結果圧密沈下が生じます。 上記の(a)及び(b)の現象に対して本プログラムでは区分なく慣用法により解法します。つまり、(b)の現象については地下水位の低下に伴う浮力消失量を自動計算し、その浮力消失量を載荷重として作用させることにより解法します。いずれも慣用法による解法であり、FEM等により土中水の挙動を解法しているわけではございませんので、その際の地盤の変形は鉛直方向の圧縮変形のみに帰着され、側方移動については見込まれませんのでご注意下さい。 Page Top 　５．地中応力 Ｑ５−１． 地中応力をオスターバーグの応力図表で計算できるか？ Ａ５−１． 「設計条件」入力画面で、「オスターバーグ応力図表」を選択していただければ可能です。 なお、この応力図表は等脚台形用に対応するものであり、載荷できる盛土形状は、原地盤面が水平であり、小段等の形状変化のない等脚台形に限定されます。 原地盤面が水平でなかったり、盛土形状においてのり面勾配が異なる場合には、地中応力の計算に際しては、ブーシネスク法を適用して下さい。 　 Ｑ５−２． オスターバーグで沈下計算を行うとき、上載荷重として交通荷重を入力することは可能か？ Ａ５−２． 本プログラムにおける載荷重の区分につきましては、この定型に対する応力図表を使用するか否かを選択するものであり、載荷重の材質が盛土であるか交通荷重であるか等の荷重の実際の種別には依存しません。 「盛土（単位重量）」とは、オスターバーグ図表用に設けている台形入力（原地盤面はフラット）用であり、この応力図表には、お問合せのような盛土天端の載荷重を含まれておりません。 オスターバーグの応力図表とは、原地盤面が水平であり盛土に小段がない、つまり載荷重形状が台形である場合に対応する応力図表です。 そのため、お問合せのように、盛土荷重と交通荷重との双方を考慮されますような任意形状の荷重につきましては、「盛土（単位重量）」ではなく、「荷重（単位重量）」にて入力して下さいますようお願い致します。 このオスターバーグの応力図表は、ブーシネスク法によって台形形状の寸法をパラメータとして図表化したものであり、両者は基本的には等価となります。 　―応力算出法― 　　●ブーシネスク法 　　○オスターバーグ図表 　―載荷重の入力― 　　●荷重（荷重強度ｑ） 　　○盛土（単位重量γ） Page Top 　６．沈下時間 Ｑ６−１． 放置期間に対する残留沈下量の検討で、放置期間はどのように考えれば良いのか。 Ａ６−１． 放置期間とは、施工開始日からの期間を指します。緩速載荷の場合には、施工期間と放置期間とを含んだ日数が放置期間になります。また段階施工のときには、1段目の施工開始日からの期間になります。（施工段階（１）が施工されてから２段目が施工されるまでの放置期間を含みます。） 　 Ｑ６−２． 圧密層の排水条件を片面排水にした場合と両面排水にした場合とでは，圧密時間が著しく異なることがあるか？ Ａ６−２． 入力される土質諸元により大きく差が生じます。 透水係数１つでその圧密速度は大きく異なりますが、両面排水と片面排水では、排水距離が両面排水とした場合、片面の１／２倍となるため時間的効果は圧密時間にも大きな影響を及ぼします。 製品helpの圧密時間の推定式　の各計算式を確認下さい。 特に、各算定式の最大排水距離に注意して下さい。 距離の２乗の関数になるため、その時間差は大きくなります。 　 Ｑ６−３． 層区分と排水距離の考え方を説明してほしい。 Ａ６−３． 層厚換算法とは、連続する両面排水層を一つの層として換算する概念となります。 この層区分はTerzaghiの圧密方程式による圧密解法における排水距離の計算に用いる概念になり、ヘルプ[計算理論と照査の方法]-[圧密時間の推定式]-[層厚換算法]にて概念図で示しておりますように、連続する粘性土層における上面及び下面において不透水層が存在するか否かにより設定します。上面及び下面がともに透水性地盤である場合には両面排水を、上面及び下面のいずれか一方に不透水層が存在する場合には片面排水となります。 例えば、粘性土層の下に不透水性の基礎岩盤が存在した場合のように、片面の透水性を完全に見込まない場合に片面排水となり、上下に存在する層が透水性であれば、その透水係数の大小に依存せず、一律に両面排水となります。 各層の圧密係数Cvについては、層厚換算する際の排水距離として反映させ、排水時間については最下層の圧密係数が支配的であるとして計算しています。 排水距離Dは、両面排水の場合、層厚の1/2で、片面排水の場合、その層厚と同じとして扱います。 つまり、両面排水の方が片面排水の場合より短時間に排水されることとなります。Terzaghiの一次元圧密方程式を無次元化した計算式にて、圧密時間tは排水距離Dの二乗に比例する量であり、両面排水の場合には上下方向への排水となるため、片面排水の場合の半分の排水距離とした計算となります。 原地盤面が舗装等により排水を制限されている場合には、間隙水は下方向への排水に制限されるとして片面排水（下側）で良いと思いますが、原地盤面が大気圧下にあり、上面からの排水もあるとして扱う場合には、両面排水として扱うことが適切であると考えます。 Page Top 　７．沈下量 Ｑ７−１． 粘土の即時沈下は計算できるか？ Ａ７−１． 「設計条件」入力画面で、「即時沈下量の算出」を選択していただければ可能です。 　 Ｑ７−２． 同じ盛土高で載荷幅を広げると、圧密沈下は大きくなるのに、即時沈下は小さくなるのはなぜ？ Ａ７−２． 盛土や構造物の載荷による地盤変形は、地盤を構成する個々の土に生ずる変形の集積として捉えられ、有限幅荷重においては経時的排水に伴う体積変化である圧密変形と、主応力差の増加に基づく体積変化を伴わない即時的なせん断変形とが重なって生じるものと考えられます。ここでいう即時沈下とはこの等体積せん断変形を指し主に荷重端部付近での変形であるため、盛土中央下部においては盛土幅もしくは奥行きが小さい方がより大きく、幅もしくは奥行きが大きくなるに従い小さくなります。 圧密沈下量：排水に伴う体積減少変形であり、載荷幅もしくは載荷奥行が大きくなる（下図中：黄色→桃色）ことにより、載荷重自体が大きくなるため、地盤の圧縮変形は大きくなります。 即時沈下量：地盤を弾性体とみなした体積変化を伴わない弾性変位量であり、載荷幅もしくは載荷奥行が大きくなる（下図中：黄色→桃色）ことにより、地盤が全体的に押されるため、地盤のせん断変形は小さくなります。 Ｑ７−３． Δe法、mv法に比べ、Cc法により算出した沈下量が過大になる理由は？ Ａ７−３． Cc 法での沈下量が過大に評価されますのは、Cc法が圧密降伏点を考慮していない理論であることに起因します。e-logP曲線の入力にて曲線の降伏箇所が認められますこと、当該地盤は過圧密状態であることが想定されます。Δe法やmv法では、地盤特性を曲線にて設定しますため、降伏地点前後での沈下特性は異なります。一方、Cc法では地盤特性を一つの定数（圧縮指数）で代表させますため、圧密降伏は考慮されません。そのため、正規圧密地盤に対してはこれらの計算結果はある程度整合しますが、過圧密地盤に対しては沈下量に大きな差が発生する場合があります。 Page Top 　８．土質データ Ｑ８−１． 沈下が発生しない岩や沈下を無視したい層が存在する場合には、どのように入力すればよいか。 Ａ８−１． 層区分として「非圧縮層」を選択してください。 　 Ｑ８−２． 地表面形状が複雑な形状をするような入力での地層入力の際の留意点は何か。 Ａ８−２． 地層モデルの取り方で複雑な形状であっても再現することが可能です。例えば、水路を埋めるような場合、モデルの両端がｙ＝０〜ｙ＝０の座標となりますが、その中間点（水路の部分）をへこませてモデル設定し、水路を埋めてその下の沈下量を計算する様な際にも、（１）層データ入力で　中間点を作成していただく�A地層のブロック化をして細かい形状を再現するにより可能です。複雑な形状も同じようにお考え下さい。 　 Ｑ８−３． データ入力で試験値（ｅ−ｌｏｇｐ）を入力すれば内部計算で初期間隙比（ｅｏ）を算出するか？ Ａ８−３． 粘性土層に対しての初期間隙比は、入力いただくｅ−ｌｏｇｐ曲線、もしくは標準圧密曲線より算出しています。また砂層の場合はB.K.Houghの図表、もしくは入力いただく砂の圧力−間ゲキ比曲線より算出しています。土質データ入力画面で「砂の圧力−間ゲキ比曲線」がチェックされていない場合、入力いただく「層区分」で選択される材料により支配されますのでご注意下さい。即ちシルトなど設計上、設計者がどちらの性質であるかと判断された場合にはこの設定により判断され設計することになります。 Ｑ８−４． 土質データ入力部分の３つの曲線入力のPは、圧密圧力か平均圧密圧力のいずれか？ Ａ８−４． 一般的にｅ-logｐ曲線におけるｐは圧密荷重を採用し、物理試験で圧密載荷試験を行った結果として得られた結果を入力頂ければよいと存じます。一方、ｍｖ−ｐ曲線は、平均圧密荷重と体積圧縮係数との関係図ですので平均圧密荷重を入力していただき作成して下さい。また、Ｃｖはｍｖの関数としても表される圧密係数ですので、ｍｖと同様にお考え下さい。 Ｑ８−５． 先行圧密応力ｑ0はどのように計算に用いられるのか？ Ａ８−５． 先行圧密応力q0につきましては、沈下量計算時（�册法，mv法，Cc法）に使用します。 q0＞0とした場合には、過圧密地盤としての沈下量の計算となり、q0＝0とした場合には、正規圧密地盤としての沈下量の計算となります。 Ｑ８−６． 地盤改良により全く沈下しない設定とする方法は？ Ａ８−６． 改良土を「非圧縮層」として設定することにより、改良土には沈下が全く発生しないとした扱いとすることができます。 また、層区分はそのままに、圧密試験（e-logP）の入力値として水平線を設定（圧密圧力に比して間隙比が変化しない）とした入力に変更することでも可です。 なお、改良土に対していくらかの沈下を認める場合には、自然地盤における圧密試験（e-logP）を改良地盤の物性値として、曲線の勾配を緩くして設定することにより、改良土が沈下するとした扱いとなります。 さて、わが国の多くの公共機関が示す設計指針類（例えば、「道路土工―軟弱地盤対策工指針」，「建築基礎構造設計指針」等）では、有限幅の荷重が載荷される場合の地盤変位に対して、個々の断面位置での地盤内鉛直方向応力を、弾性論を用いて算定し、その鉛直応力によって生じる鉛直方向の圧密沈下量を一次元圧密理論によって算定する方法が示されており、一般的な構造物の設計では、この手法が今日でも多用されています。 　ここで、Terzaghiの圧密理論は、もともと側方の変形が完全に拘束された一次元圧密を取り扱っており、載荷幅が大きい場合においては妥当性を有していますが（上図の中央付近における変形量）、せん断変形を生じるような有限幅の載荷に対しては、設計指針類に準拠した一次元圧密理論による計算のみでは、必ずしもこのような変形機構を十分に再現できるとは限りません。 　ＦＯＲＵＭ８製品では、せん断変形を伴う地盤変位量の算定に際して、別途、地盤を弾性体とみなし弾性変位量として即時沈下・側方変位を算出する機能を設けることにより、この問題点を解消しています。これにより、ＦＯＲＵＭ８製品では設計指針類に準拠した圧密沈下計算を採用しながら、かつ、必要に応じてせん断変形の影響照査も可能であり、これらを一連の計算書として出力します。  >> サポートページ　圧密沈下の計算　Ｑ＆Ａ集

Page Top